LA PARÁBOLA
En matemáticas, una parábola (del griego παραβολή) es la sección cónica de excentricidad igual a resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz,y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.
La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
|
Semejanza de todas las parábolas
Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad . La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Tangentes a la parábola
|
:
Ecuaciones de la parábola
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y = ax2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo»Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.
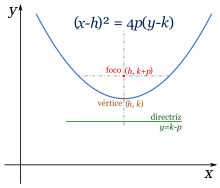
Ecuación involucrando la distancia focal
Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:
|
Ecuación general de una parábola
Hasta ahora se han descrito solo parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x o de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.
|


 . La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.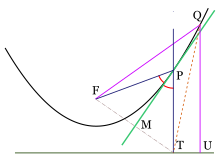

 .
.

No hay comentarios:
Publicar un comentario