la circunferencia

LA CIRCUNFERENCIA

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante que se denomina radio.

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• Centro: Es el punto interior equidistante de todos los puntos de la circunferencia;
• Radio: Es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio mide la mitad del diámetro.El radio es igual a la longitud de la circunferencia dividida entre 2π.
• Diámetro: El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia y pasa por el centro. El diámetro mide el doble del radio. El diámetro es igual a la longitud de la circunferencia dividida entre π.
• Cuerda: La cuerda es un segmento que une dos puntos de la circunferencia. El diámetro es la cuerda de longitud máxima.
• Recta secante: Es la línea que corta a la circunferencia en dos puntos.
• Recta tangente: Es la línea que toca a la circunferencia en un solo punto.
• Punto de Tangencia: es el punto de contacto de la recta tangente con la circunferencia.
• Arco: El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia. Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.
• Semicircunferencia: cada uno de los dos arcos delimitados por los extremos de un diámetro.

Longitud de la circunferencia[editar]

El interés por conocer la longitud de una circunferencia surge en Babilonia (actual Irak), cuando usaban los carros con rueda, era primordial relacionar el diámetro o radio con la circunferencia.⁷ La longitud ${\displaystyle \ell }$ de una circunferencia es:

${\displaystyle \ell =2\pi r=\pi d}$

donde r es la longitud del radio y d=2r es el diámetro. Así pues ${\displaystyle \pi \,}$ (número pi) es, por definición, el cociente entre la longitud de la circunferencia y el diámetro:

${\displaystyle \pi ={\frac {\ell }{d}}={\frac {\ell }{2r}}}$

Área del círculo delimitado por una circunferencia

Arquímedes, en su tratado Sobre la medida del círculo, definió que el área del círculo era igual en área a un triángulo rectángulo, siendo uno de sus catetos la longitud ${\displaystyle \ell }$ de la circunferencia y el otro el radio r. Así, el área del círculo delimitado por la circunferencia es:

Ecuaciones de la circunferencia[editar]

Ecuación en coordenadas cartesianas[editar]

circunferencia de radio dos en un sistema de coordenadas

En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}\,}$.

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica a

${\displaystyle x^{2}+y^{2}=r^{2}\,}$.

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia se deduce que:

${\displaystyle x^{2}+y^{2}+Dx+Ey+F=0\,}$

resultando:

${\displaystyle a=-{\frac {D}{2}}}$

${\displaystyle b=-{\frac {E}{2}}}$

${\displaystyle r={\sqrt {a^{2}+b^{2}-F}}}$

Si conocemos los puntos extremos de un diámetro: ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})\,}$, la ecuación de la circunferencia es:

${\displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.\,}$

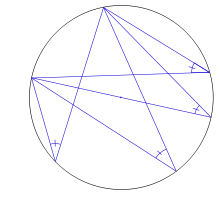
Ángulos en una circunferencia[editar]

Ángulos en la circunferencia.

Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

Un ángulo, respecto de una circunferencia, pueden ser:

Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.

La amplitud de un ángulo central es igual a la del arco que abarca.

Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)

Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

Ángulo interior, si su vértice está en el interior de la circunferencia.

La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

Ángulo exterior, si tiene su vértice en el exterior de la circunferencia